Klemperer rosette

A simple hexagonal rosette with two kinds of body, which Klemperer notes is the nearest to being stable.

The simplest system is three bodies in each other's Lagrangian points each with the same elliptical orbit; it is the only configuration known to occur naturally. Klemperer called this a "rhombus" instead of a "rosette".

A Klemperer rosette is a gravitational system of (optionally) alternating heavier and lighter bodies orbiting in a symmetrical pattern around a common barycenter. It was first described by W.B. Klemperer in 1962, and is a special case of a central configuration.

Klemperer described rosette systems as follows:

Such symmetry is also possessed by a peculiar family of geometrical configurations which may be described as "rosettes". In these an even number of "planets" of two (or more) kinds, one (or some) heavier than the other, but all of each set of equal mass, are placed at the corners of two (or more) interdigitated regular polygons so that the lighter and heavier ones alternate (or follow each other in a cyclic manner).

The simplest rosette would be a series of four alternating heavier and lighter bodies, 90 degrees from one another, in a rhombic configuration [Heavy, Light, Heavy, Light], where the two larger bodies have the same mass, and likewise the two smaller bodies have the same mass, all orbiting their (empty) geometric center. The more general trojan system has unequal masses for the two heavier bodies, which Klemperer also calls a "rhombic" system, and which is the only version that is not symmetric around the gravitational center.

The number of "mass types" can be increased, so long as the arrangement is symmetrical and cyclic pattern: e.g. [ 1,2,3 ... 1,2,3 ], [ 1,2,3,4,5 ... 1,2,3,4,5 ], [ 1,2,3,3,2,1 ... 1,2,3,3,2,1 ], etc.

Klemperer's article specifically analyzes regular polygons with 2–9 corners – dumbbell-shaped through nonagon – and non-centrally symmetric "rhombic rosettes" with three orbiting bodies, the outer two stationed at the middle orbiting body's triangular points (L4 and L5), which had already been described and studied by Lagrange in 1772. Systems with an even number of 4 or more corners can have alternating heavy and light masses at the corners, although the possible range of mass ratios is constrained by para-stability requirements; systems with odd numbers of corners must have equal masses at every corner. While Klemperer notes that all the rosettes and the rhombus are vulnerable to destabilization, the hexagonal rosette is the most nearly stable because the "planets" sit in each other's semi-stable triangular Lagrangian points, L4 and L5.

The regular polygonal configurations ("rosettes") do not require a central mass (a "sun" at the center is optional, and if present it may bobble above and below the orbital plane), although a Lagrange-type rhombus does. If a central body is present, its mass constrains the ranges for the mass-ratio between the orbiting bodies.

Misuse and misspelling

A pentagonal rosette as described in Larry Niven's novel Ringworld.

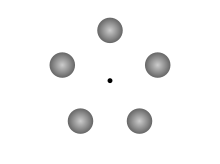
The term "Klemperer rosette" (often misspelled "Kemplerer rosette") is often used to mean a configuration of three or more equal masses, set at the points of an equilateral polygon and given an equal angular velocity about their center of mass. Klemperer does indeed mention this configuration at the start of his article, but only as an already known set of equilibrium systems before introducing the actual rosettes.

In Larry Niven's novel Fleet of Worlds in the Ringworld series, the Puppeteers' eponymous "Fleet of Worlds" is arranged in such a configuration which Niven calls a "Kemplerer rosette"; this (possibly intentional) misspelling is one possible source of the wider confusion. It is notable that these fictional planets were maintained in position by large engines, in addition to gravitational force.

Instability

Both simple linear perturbation analysis and simulations of rosettes demonstrate that such systems are unstable: Klemperer explains in his original article, any displacement away from the perfectly symmetrical geometry causes a growing oscillation, eventually leading to the disruption of the system. The system is unstable regardless of whether the center of the rosette is in free space, or is in orbit around a central star.

The short-form reason for the instability is that any perturbation corrupts the geometric symmetry, which increases the perturbation, which further undermines the geometry, and so on. The longer explanation is that any tangential perturbation brings a body closer to one neighbor and further from another; the gravitational imbalance becomes greater towards the closer neighbor and less for the farther neighbor, pulling the perturbed object further towards its closer neighbor, amplifying the perturbation rather than damping it. An inward radial perturbation causes the perturbed body to get closer to all other objects, increasing the force on the object and increasing its orbital velocity – which leads indirectly to a tangential perturbation and the argument above.

External links

• Jenkins, Bob. "Klemperer rosettes". burtleburtle.net. Physics. Retrieved 2007-01-12. — Rosette simulations

• "Kemplerer (Klemperer) rosette by Larry Niven from Ringworld". technovelgy.com.